Rokning 1c - Lærarabók - page 112-113

113 112
Egin hugskot
kann verða fatað sum 5+6+7, 56+7 ella
5+67
Dømi um uppgávur:
n Finn tað nummarið, sum gevur tann
hægsta summin.
n Finn tað nummarið, sum gevur tann
lægsta summin.
n Finn tað nummarið, har summurin er
næst 50.
n Finn tað nummarið, har summurin er
næst 100.
Nýtið sifrini og additión og sub­traktión.
Roynið at raka so nær 15, sum til ber.
Spæl: Sparigrísurin
Luttakarar: 2
Tilfar: Tveir terningar í hvør sínum liti,
spæli­pengar (Avritssíða 59–61 í
Avrits­mappu 1–4), ein teknaðan spari­grís
á pappíri ella tann á síðu 89 í næminga­
bókini.
Inn í hvønn sparigrís skulu næm­ing­arnir
leggja ein hundrað­krónu­seðil, ein
fimmti­krónuseðil, eina tjúgukrónu, tvær
tíggjukrónur, tvær fimmkrónur og
tríggjar einkrónur.
Spælið fer fram soleiðis, at spælararnir
skiftast at ringla við báðum terningum
við hvør sínum liti, har annar liturin
um­boðar tíggjarar og hin eittarar. Er
annar terningurin t.d. reyður og
um­boðar tíggjarar, og hin hvítur og
um­boðar eittarar, og tann reyði vísir 4
og tann hvíti 5, so skal tann, sum
ringlaði, fáa 45 krónur frá hinum. Tann,
sum fyrst missir allar pengarnar ella
hevur minst eftir, tá ið tíðin er farin,
hevur tapt.
Høvuðbrot
Avritssíður 44, 92–94, 98–107 og 3.9b
í Avritsmappu 1–4.
Størri avbjóðing
Tá ið næmingarnir hava roknað upp­
gávurnar í bókini, kunnu teir velja sær
tvey tøl millum 10 og 30 at gera
additións­stykki burturúr. Bæði upp­gávan
og mátin, tey hugsa til at rokna hana,
skulu verða skrivað í kladdu­heftið.
Høvuðbrot
Avritssíður 44 og 98–107 í Avrits­mappu
1–4 .
Annað virksemi
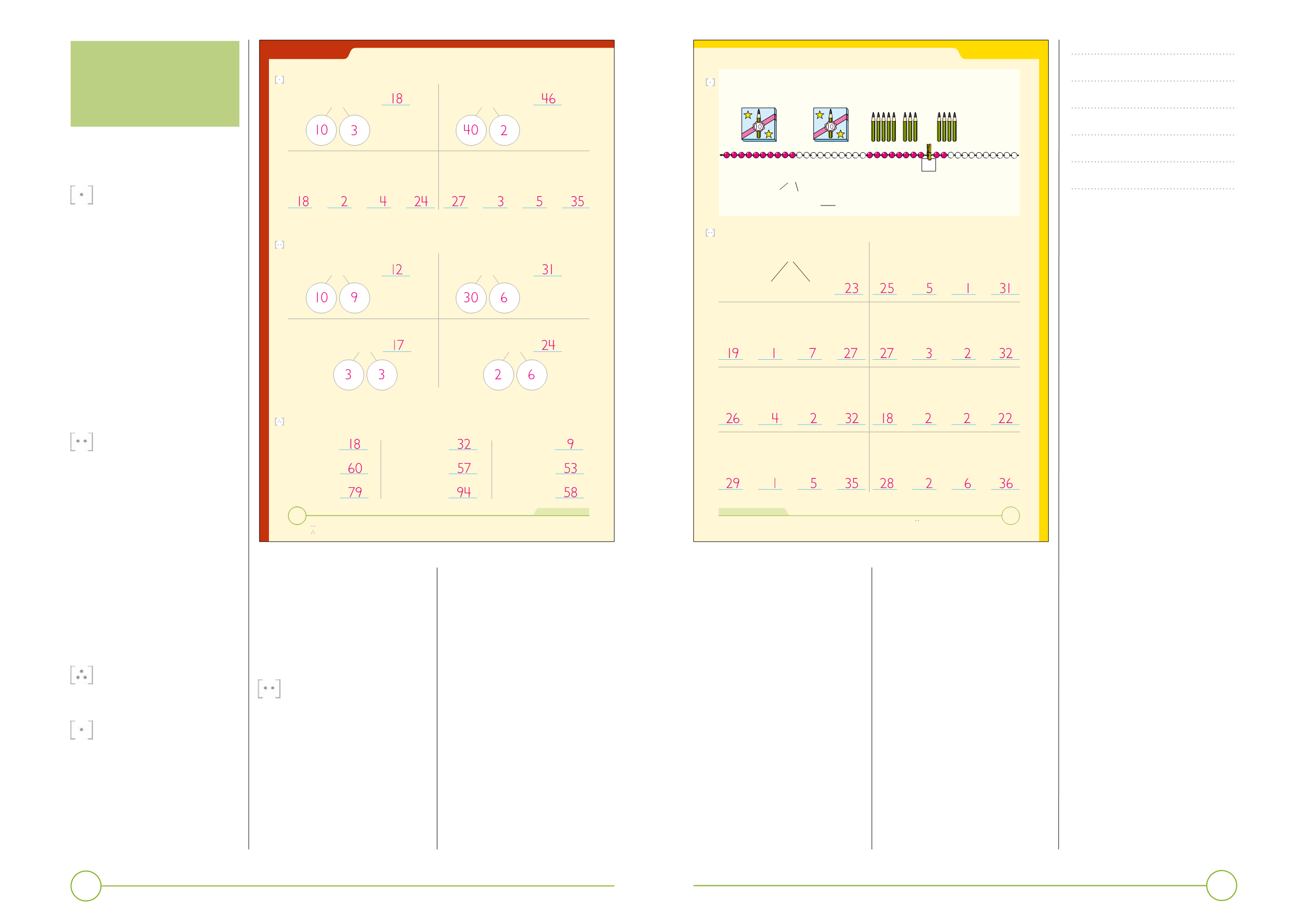
Nummarplátur
Lat næmingarnar fara út at savna tøl á
nummar­plátum. Sifrini í tølunum kunnu
verða nýtt eitt og eitt ella sett saman til
tveysifrað tøl. Hvat loysir seg best,
mugu næmingarnir taka støðu til fyri
hvørja einstaka uppgávu. Dømi: 567
kubbar í 28 fyri at hava 3 tíggjara­stavar.
Við blýantunum á myndini kunnu vit
taka 2 blýantar og leggja aftur at teimum
8 „leysu“ fyri at fáa ein pakka við tíggju
í. Á perlu­band­inum leypa vit tvær kúlur
til høgru frá 28 at koma til 30.
Síðan nýta vit talvinir til at finna talið
á eittarum, sum eru eftir og skulu verða
lagdir afturat. Í døminum eru 2 eftir, tá
ið vit hava brúkt 2 til at fylla upp til
tíggjaran (eftirsum 2+2=4).
Best er, um næmingarnir fata, hvussu
hetta arbeiðið við ítøkiligum lutum kann
verða skrivað sum roknistykki í bókini.
Men halda næm­ing­arnir hendan mátan
at skriva vera ov torskildan, so er eingin
orsøk at royna at venja hann. Tað, sum
um ræður, er, at tey, tá ið tey skulu
rokna, duga at nýta tað, sum tey vita um
tíggjara­vinir og talvinir og um at taka tøl
sundur í tíggjarar og eittarar.
uppgávur sum hesar í høvd­inum. Lærarin
eigur kortini at mæla næmingum, sum
rokna í høvdinum, til at taka tað seinna,
eittsifraða talið sundur, sum víst í
døm­inum. Tað ger næmingarnar
med­vitandi um sín egna roknihátt og
eggjar teimum til at nýta munabetri
hættir. Hetta er serliga galdandi fyri
næm­ingar, sum telja seg fram til svarið.
Einfaldari
Vís við ítøkiligum lutum, hvussu vit
kunnu leggja slík tøl saman við at byrja
við tí fyrra, tí tveysifraða talinum og
leggja aftur at tí upp til næsta heila
tíggjara. At gera hetta mugu næm­ing­
arnir duga tíggjaravinirnar: Í døminum
mugu vit byrja við at leggja 2 afturat, tí
at í 28 eru 8 eittarar, og 2 er tíggjara­
vinur hjá 8. Við tíggjarastavum resta 2
síðuni ber til at rokna allar upp­gávur­nar
á ein ávísan hátt, sum er at taka tað
eittsifraða talið sundur, so at eitt heilt
tal av tíggjarum verður burtur úr tí
tveysifraða talinum saman við tí fyrra av
tí sundurtikna talinum. Lærarin eigur at
vísa, hvussu hetta verður gjørt.
Legg saman
Tak tað seinna talið sundur í tvey,
so tað verður eitt heilt tal av tíggj­arum
burtur úr tí fyrra talinum.
Vita næmingarnir svarið í høvd­inum,
áðrenn teir hava skrivað millum­
rokningina, so er tað í lagi. Bið tá
næmingarnar greiða frá, hvussu teir
gjørdu. Tað er t.d. lætt at rokna 28+8
við at leggja 10 aftur at 28 og síðan
draga 2 frá.
Millumrokningarnar eru einans
ætlaðar sum hjálp til at rokna additións­
Støddfrøðiligt innihald
n Additión og subtraktión við
eittsifraðum og tveysifraðum
tølum, við og uttan tíggjaraskifti
Hvat er at gera?
 Síða 112 Roynd
Rokna additións­
uppgávurnar
Rokna svarini á additiónsuppgávunum. Í
ovara raðnum eru uppgávur við ongum
tíggjaraskifti. Her skulu næmingarnir
umframt at rokna seg fram til svarið
taka tað tveysifraða talið sundur í
tíggjarar og eittarar. Í niðara raðnum eru
uppgávur við tíggj­ara­skifti. Her kunnu
næmingarnir annað­hvørt taka tað fyrra
ella tað seinna talið sundur sum hjálp at
finna svarið.
Skriva næmingarnir bara tað rætta
svarið og vísa ikki millumrokningar, so
er tað í lagi. Millumrokningin er einans
ætlað sum hjálp at loysa uppgávur av
hesum slagnum í høvdinum.
Rokna
subtraktiónsuppgávurnar
Rokna svarini á sub­traktións­upp­gávu­
num. Í tí ovara raðnum eru uppgávur við
ongum tíggjaraskifti. Her skulu næm­ing­
arnir umframt at rokna seg fram til
svarið taka tað tveysifraða talið sundur í
tíggjarar og eittarar. Í niðara raðnum eru
uppgávur við tíggjara­skifti. Her skulu
næmingarnir taka tað seinna talið
sundur sum hjálp at finna svarið.
Skriva næmingarnir bara tað rætta
svarið og vísa ikki millumrokningar, so
er tað í lagi. Millumrokningin er einans
ætlað sum hjálp at loysa uppgávur av
hesum slagnum í høvdinum.
Rokna
Rokna svarið á uppgávunum.
 Síða 113 Venjing 1
Samrøðumynd um at
leggja eittsifrað og
tveysifrað tøl saman,
við tíggjaraskifti
Les uppgávuna fyri næmingunum og bið
teir finna ymiskar mátar at rokna hana.
Bið næmingarnar siga hvørjum øðrum,
hvussu teir gera. Hvønn máta dámar tær
best? Hví?
Greið næmingunum frá, at á hesari
Roynd
• 112 6 • Pluss og minus
Rokna.
Rokna.
Rokna.
14 + 4 = 25 + 7 = 18 – 9 =
52 + 8 = 48 + 9 = 58 – 5 =
73 + 6 = 87 + 7 = 63 – 5 =
13 + 5 = 42 + 4 =
18 + 6 =
+ + =
27 + 8 =
+ + =
19 – 7 = 36 – 5 =
23 – 6 = 32 – 8 =
Næmingarnir brúka samanleggingarmannagongdir, sum teir hava arbeitt við í hesum kapitlinum, at loysa uppgávurnar.
Næmingarnir brúka frádráttarmannagongdir, sum teir hava arbeitt við í hesum kapitlinum, at loysa uppgávurnar.
Rokna og skriva úrslitini.
Prøve
•
www.snar.fo/rokning 113
Samrøðumynd um samanlegging við tveysifraðum og eittsifraðum tølum við tíggjaraskifti. Við uppgávunum menna
næmingarnir høvurokning viðvíkjandi samanlegging við fleirsifraðum og eittsifraðum tølum við tíggjaraskifti.
Rokna.
Venjing 1
Hákun hevur 28 blýantar. Hann keypir 4 blýantar afturat.
Hvussu nógvar blýantar hevur hann so?
28 + 4 =
28 + 2 + 2 = 32
17 + 6 =
17 + 3 + 3 =
25 + 6 =
+ + =
19 + 8 =
+ + =
27 + 5 =
+ + =
26 + 6 =
+ + =
18 + 4 =
+ + =
29 + 6 =
+ + =
28 + 8 =
+ + =
28