Rokning 1c - Lærarabók - page 104-105

105 104
næmingarnir verða hildnir til at finna
góðar mátar at rokna. Tað hevur størri
týdning, enn at tey fáa upp­gávurnar
skjótt frá hondini.
Næmingarnir kunnu gera nakrar
upp­gávur afturat við at nýta talkort frá 1
til 9. Tey taka tvey kort úr rúgvuni og
seta saman til eitt tvey­sifrað tal, og
síðan taka tey tvey kort aftur­at og seta
tey saman til eitt nýtt tvey­sifrað tal. So
leggja tey tølini saman og skriva
roknistykkið í kladdu­heftið hjá sær.
Annað virksemi
Spæl: Tvey spæla saman
við snariskivu
Sí Ískoyti 2 aftast í hesari bókini.
Munurin er, at á síðu 105 er tíggjara­
skifti. Men um næmingarnir nýta ítøkiligt
tilfar, kunnu tey veksla tíggju eittarar til
ein tíggjara og síðan telja talið á
tíggjarum og eittarum.
Á Avritssíðu 93b í Avritsmappu 1–4
eru uppgávur, har næmingarnir skulu
leggja heilar tíggjarar saman við
eitt­arum, sum t.d. 50+8=
Størri avbjóðing
Legg eitt siffur afturat framman fyri tað
seinna talið í hvørjari uppgávu, so at
næmingarnir skulu leggja tvey tvey­sifrað
tøl saman. Við at leggja eitt siffur afturat
frammanfyri er framvegis einki
tíggjaraskifti í uppgávunum á síðu 104,
og tær á síðu 105 hava framvegis
tíggjaraskifti.
Tað hevur stóran týdning, at
best at taka sundur so­leiðis, at fyrri
liður saman við tí fyrsta talinum í
uppgávuni verður ein tíggj­ari. Tann fyrsta
uppgávan er 15+9. Her resta 5 í at
røkka einum heilum tíggjara (15+5=20).
Tí er best at taka 9 sundur í 5+4.
Einfaldari
Lat næmingarnar loysa uppgávurnar við
kubbum/sentiterningum/base 10-tilfari
ella við pengum (tíggju­krónum og
einkrónum). Gera tey tað, so eiga tey
aftaná at verða hjálpt til at síggja, hvussu
tað, sum tey hava gjørt við ítøkiligum
lutum, kann vera um­boðað av talstavum
og skrivað í bókina.
Hjá hesum næmingum kann vera
frægari at nýta tann háttin, sum er vístur
vinstrumegin ovast á síðu 105, eftir­sum
tað er sami háttur sum á síðu 104.
n Hví tekur Bifla 7 sundur í 4+3? Kundi
hon ikki tað sama tikið 7 sundur í 5+2?
(Jú, tað kundi hon, og so roknað
26+5=31 og 31+2=33. Men tølini
verða einfaldari, um hon brúkar 4+3, tí
har resta 4 í 26 at fáa ein heilan tíggjara
(4 og 6 eru tíggjaravinir).Tá ið hon
dregur 4 frá 7, eru 3 eftir, sum hon
leggur afturat at enda.)
Legg saman
Rokna svarini á uppgávunum.
Næmingar­nir verða bidnir um at taka
annað­hvørt tað fyrra ella tað seinna
talið sundur í tvey, og so skriva eins og í
øðrum av dømunum. Verður tað fyrra
talið tikið sundur, er best at taka sund­ur
í tíggjarar og eittarar. Síðan verða
eittararnir lagdir saman og verða at
enda lagdir saman við tíggjarunum.
Verður tað seinna talið tikið sundur, er
at tað týdningarmesta er mátin , sum
verður brúktur at rokna: Tú vilt fegin
vita, hvussu næmingarnir rokna, og ikki
endiliga, hvat svar tey fáa. Tað at fáa
næmingarnar at tosa um og greiða frá
mátanum, sum tey brúka at rokna við,
er eitt sera hent amboð til læring. Ofta
er tað soleiðis, at ikki fyrr enn tú greiðir
onkrum øðrum frá einum­hvørjum, skilir
tú tað sjálv/ur.
Tað eru ymsir mátar at loysa hesa
upp­gávuna, men teir eru í høvuðs­heitum
brigdi av teimum báðum mát­unum, sum
eru vístir í døminum. Í tí fyrra mátanum
verða tølini tikin sundur í tíggjarar og
eittarar, sum so verða viðgjørdir hvør
fyri seg. Hesin mátin samsvarar við tað,
sum vit gera í skrivligum algoritmum.
Hin mátin byggir á at telja víðari frá tí
fyrra talinum; ein máti, sum ofta er
hentur at nýta í høvuðrokning.
Hvat er at gera?
 Síða 104
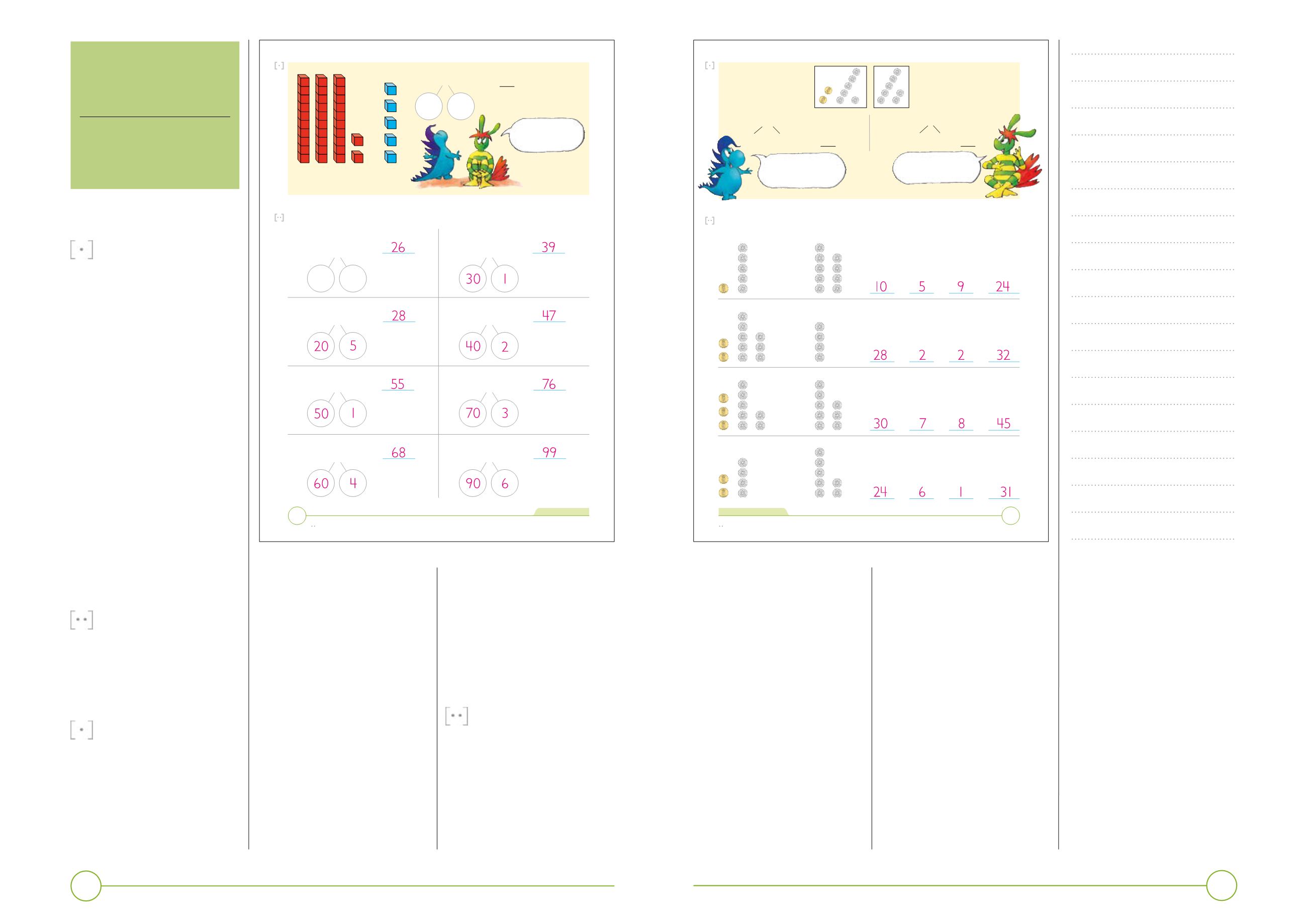
Samrøðumynd um at
leggja saman tveysifrað og
eittsifrað tøl uttan tíggjaraskifti
Tosa við næmingarnar um dømið ovast
á síðuni. Serliga ræður um at minna tey
á, hvussu vit kunnu taka tveysifrað tøl
sundur í tíggjarar og eitt­arar. Her er tað
gjørt við kubbum, og á síðu 105 er tað
gjørt við pengum.
Næmingarnir skulu fyrst taka tað
tvey­sifraða talið sundur í tíggjarar og
eittarar. Tey skulu skriva tíggjararnar við
talvirðinum, ikki bara sifrið (altso 30,
ikki 3 tíggjarar). Síðan leggja tey saman.
Á hesari síðuni verður arbeitt við, at
næmingarnir skulu leggja eitt­ararnar
saman fyri seg og síðan leggja
tíggjararnar afturat. Kanska eru summ­ir
næmingar, sum rokna upp­gávuna í
høvdinum og skriva svarið fyrst og síðan
taka tað fyrra talið sundur í tíggjarar og
eittarar. Tað er í lagi at gera soleiðis,
eftirsum hesin mátin at skriva ikki er
ætlaður sum ein algoritma, ið
næmingarnir skulu læra, men stuðul til
at rokna í høvdinum.
Legg saman
Næmingarnir skulu taka tað
tvey­sifraða talið sundur í tíggjarar og
eitt­arar, áðrenn tey finna svarið við fyrst
at leggja eittararnar saman og síðan
leggja tíggjararnar afturat.
 Síða 105
Samrøðumynd um at
leggja saman tveysifrað og
eittsifrað tøl við tíggjaraskifti
Tosa við næmingarnar um, hvussu til
ber at loysa uppgávuna 26+7. Næm­ing­
arnir eiga at fáa høvi at loysa upp­gávuna
sjálvir, áðrenn tey hyggja at mát­unum,
sum verða vístir í døminum. Meðan
arbeitt verður við hesum báðum
síðunum, eigur lærarin at leggja dent á,
6 • Pluss og minus
104
32 + 5 = 37
30 2
24 + 2 = 31 + 8 =
25 + 3 = 42 + 5 =
51 + 4 = 73 + 3 =
64 + 4 = 96 + 3 =
20 4
Eg leggi eittarar
saman fyri seg:
2 + 5 = 7
Hvussu nógv er til samans?
• Samrøðumynd um at leggja saman eittsifrað og tveysifrað tøl við ongum tíggjaraskifti.
Við hesum uppgávunum venja næmingarnir høvuðrokning og hetta slagið av samanlegging.
www.snar.fo/rokning 105
• Samrøðumynd um at leggja saman tveysifrað og eittsifrað tøl við tíggjaraskifti.
Við hesum uppgávunum venja næmingarnir høvuðrokning og hetta slagið av samanlegging.
26 + 7 = 26 + 7 =
20 + 6 + 7 = 33 26 + 4 + 3 = 33
Hvussu nógv er tað til samans?
15 + 9 =
+ + =
28 + 4 =
+ + =
37 + 8 =
+ + =
24 + 7 =
+ + =
Eg taki 7 sundur í 4 + 3.
Tá fái eg 26 + 4 = 30 og
30 + 3 = 33.
Eg taki 26 sundur í tíggjarar
og eittarar og fái 20 + 6.
6 + 7 = 13 og
20 + 13 = 33.
Egin hugskot
Støddfrøðiligt innihald
n Legg saman tveysifrað og
eittsifrað tøl við og uttan
tíggjaraskifti
Tilfar/amboð
n Spælipengar
n Base 10-tilfar, sentiterningar,
litstavar og tílíkt