11
10
Egin hugskot
hvørji tøl teir halda koma aftan á 20, og
hvussu tey verða skrivað. Niðurstøðuna
kunnu vit gera í felag og skriva á talvuna:
Soleiðis skriva vit tøl størri enn 20.
Einfaldari
Tað eru fleiri mátar at gera hetta spælið
einfaldari. Vit kunnu mæla næmingunum
til at brúka eina tallinju. Er tað ov
torført, kunnu tey telja á einum
perlubandi, ella tey kunnu telja eyguni á
terningunum. Tað ber eisini til at strika
ein punt, so at næmingarnir skulu brúka
tríggjar puntar í staðin fyri fýra. So
verður summurin hægst 18.
Størri avbjóðing
Lat næmingarnar spæla spælið á síðu 11
fleiri ferðir. Tað kann verða víðkað til at
Síða 11
Additión við samanseting
Næmingarnir telja eyguni á
terningunum og leggja saman. Vís á
teknið fyri pluss. Hava næmingarnir sæð
hetta áður? Minnast tey, hvat tað
merkir?
Nýt høvið at tosa við næmingarnar
um, hvussu tey kunnu koma fram til
svarið. Hvussu rokna teir einstøku
næmingarnir?
Summi telja øll eyguni og finna svarið
soleiðis.
Summi telja kanska frá øðrum talinum
og so víðari, t.d.: fimm, … seks, sjey,
átta.
Summi eru farin at duga hetta uttanat
og vita bara rætta svarið.
Í øllum uppgávunum vísa báðir
terningarnir tað sama: 1+1, 2+2, 3+3
o.s.fr. At læra seg tvífalding av hesum
plássinum.Við ongum 0 stendur 1 uttast
høgrumegin, altso á eittaraplássinum.)
Okkum tørvar so statt eitt
tekn
at vísa
eitt
tómt pláss.
Í 10 hava vit t.d. ongan
eittara, bara ein heilan tíggjara. Ikki er
neyðugt at gera so nógv burtur úr
hesum nú; tað verður gjørt seinni.
Í tóma rútin skulu næmingarnir tekna
10 lutir. Næmingarnir skulu eisini læra
seg at skriva tølini 10 og 0. Ansa væl
eftir, at tey skriva rættan veg.
At telja
Næmingarnir skulu telja, hvussu
nógvar blómur eru av hvørjum slagi, og
skriva rætta talið í rútin høgrumegin.
Hvat er at gera?
Síða 10
Lær at skriva taltekn
Tosa við næmingarnar um ymsar
mátar at vísa 10. Spyr næmingarnar:
n
Vita tit um okkurt, sum tíggju eru av?
(Dømi: 10 fingrar, 10 tær, 10 egg í einum
eggjabakka, 10 blýantar í einum pakka,
10 krónur í einari tíggjukrónu.)
n
Hvat skulu vit ringla við tveimum
terningum fyri at fáa tíggju?
Legg dent á, at talið 10 er serstakt. Tað
má verða skrivað við tveimum sifrum, tí
vit hava ikki fleiri talstavir. Í staðin gera
vit ein tíggjarabólk. So statt merkir sifrið
1 nú ikki eitt, tí har stendur eitt siffur
høgrumegin. Sifrið 1 stendur á
tíggjaraplássinum og sigur, at vit hava ein
tíggjara. Tað næsta talið er ein tíggjari og
ein eittari, altso 11. Nýt ítøkiligar lutir at
gera hetta sjónligt t.d. „base 10“-tilfar,
litstavar (cuisenaire) og krónur og
tíggjukrónur. Hetta verður gjølla viðgjørt
seinni í kapitlinum.
Ovast á síðuni er ein tallinja, har øll
tølini upp í 10 nú eru merkt við bláum.
Hetta kann vera støði undir einari
samrøðu um tølini, sum koma aftan á
10, altso 11, 12 o.s.fr. upp í 20.
Sifrið 0
er eisini serstakt. Tosa við
næmingarnar um tað at vísa á eitt tal á
lutum, tá ið vit ongan lut hava. Á
tekningini skulu eingir puntar litast, og
har skal eingin tekning vera í tí stóra
rúminum. Á tallinjuni kunnu vit vísa á 0
við at tosa um, hvat er eitt minni enn 1.
n
Talið tíggju skriva vit „eitt null“ (10).Tað
merkir ein tíggjari og eingin eittari. Hava
vit ongan eittara, kunnu vit so ikki bara
lata vera við at skriva nullið? (Nei, okkum
tørvar 0 at standa á plássinum og vísa,
at sifrið 1 skal standa á tíggjara
Hvussu nógv?
0
1
2
3
4
5
6
7
9
10
8
0
null
0
1
2
3
4
5
6
7
9
10
8
10
tíggju
1•Tølini 0–20
10
•
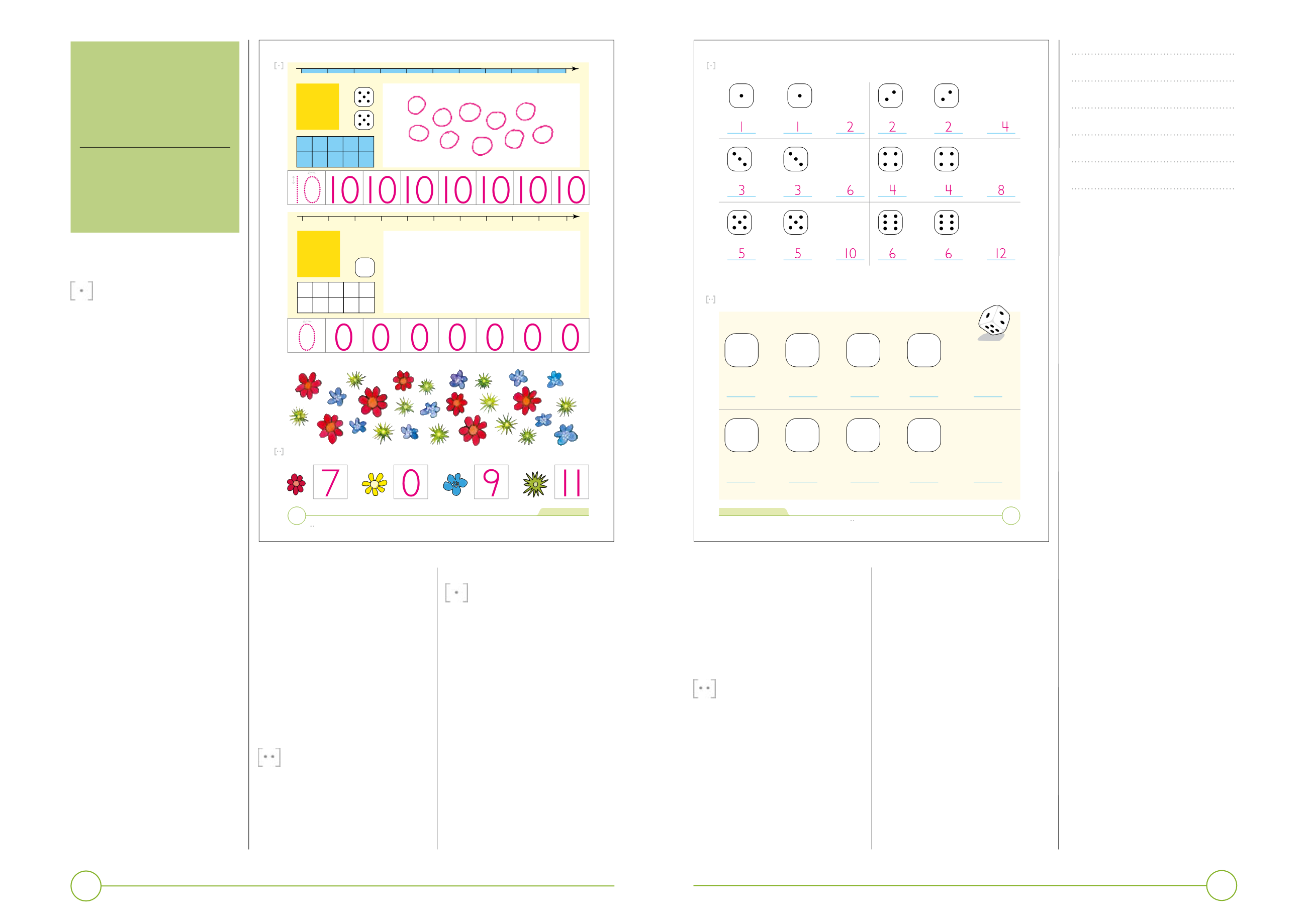
Tekna rætta talið á lutum í rútin og skriva tølini. Ger tær ómak, tá ið tú skrivar tølini – hygg at fyrimyndini.
Tel og skriva tøl í rútarnar.
Hvussu nógv eygu eru til samans?
Spæl: Hvør fær mest?
+
+
+
=
+
+
+
=
11
•
Tel eygu á terningunum og skriva bæði roknistykki og svar.
Ringla við einum terningi. Tekna eyguni, sum tú fært, á
terningarnar í bókini og skriva talið á strikuna undir terningunum. Eftir fýra umfør leggja spælararnir síni úrslit saman.
Tann, sum hevur størsta talið, hevur vunnið.
+
=
+
=
+
=
+
=
+
=
+
=
slag er ofta tað fyrsta, sum næmingar
læra uttanat av additión. Legg dent á,
hvussu hent tað er at duga sovorðið
uttanat: So verður tað nógv skjótari at
rokna. At telja seg fram fyri at loysa 4+4
kann harafturímóti vera strævið, og tú
kanst eisini lættliga telja skeivt.
Spæl:
Hvør fær meiri?
Luttakarar: 2
Tilfar: Ein terningur
Her skulu næmingarnir ringla fýra ferðir
við einum terningi og hvørja ferð skriva
tal á eygum. At enda leggja tey saman.
Vinnari er tann, sum fær hægsta talið til
samans. Tað kann vera hent fyrst at gera
hetta í felag.
Úrslitið á roknistykkjunum kann
gerast meiri enn 20. Vit eiga at mæla
næmingunum til at tosa saman um,
ringla fimm ferðir, ella tey kunnu brúka
ein terning við tíggju síðum fyri at fáa
størri tøl í hvønn punt.
Ger roknistykki
Lat næmingarnar brúka talkort ella
vanlig spælikort at gera roknistykki. Tey
kunnu arbeiða saman tvey og tvey.
Hvørt par fær talkort frá 1 til 9
(Avritssíða 63 í
Avritsmappu 1–4
) ella
eini spælikort við kortunum frá 1 (essi)
til 9. Næmingarnir kunnu sjálvir velja
sær kort at gera roknistykki úr, ella teir
kunnu taka tilvildarliga úr rúgvuni.
Lærarin kann tekna eina tallinju upp í 20
á talvuna. So kunnu næmingarnir brúka
hana at telja seg fram og vita, hvussu
tølini verða skrivað.
Annað virksemi
Spæl:
Tvífalding pluss eitt
Luttakarar: 2
Tilfar: Ein terningur, litblýantar í
tveimum ymiskum litum og eitt talrað
við tølunum frá 2 til 13:
2 3 4 5 6 7 8 9 10 11 12 13
Næmingarnir skiftast at ringla. Næming
urin tvífaldar talið á eygum. So kann
hann velja, um hann vil leggja eitt afturat
ella hava talið sum tað er. Um hann fær
2, kann hann strika 4 ella 5. Um hann
fær 5, kann hann strika 10 ella 11. Hvør
hevur sín litblýant at strika við.
Móti endanum á spælinum kann tað
vera, at báðir møguleikar longu eru
strikaðir. So má næmingurin bíða til
næstu ferð; hann kann einki strika
hesaferð. Spælið er liðugt, tá ið øll tølini
eru strikað út, ella tá tíðin er farin.
Vinnari er tann, sum hevur flestar
útstrikingar í sínum liti.
Spæl:
Dupult-bingo
Sí Ískoyti 1 aftast í bókini.
Støddfrøðiligt innihald
n
Talstavirnir 10 og 0
n
Finna tal á lutum við at vita, at
tá ið talt verður, er tað seinasta
talorðið, sum ásetur mongdina
n
Tvífalding
Tilfar/amboð
n
Ein terningur
n
Møguliga tallinja, perluband
og talkort


