Rokning 1c - Lærarabók - page 38-39

39 38
so endaði klemman her. Fyri at finna út
av, hvat talið er, síggja vit, at tað er ein
tíggjari og trý afturat, altso 13.
Størri avbjóðing
Lat uppgávu á síðu 39 gerast eina
størri avbjóðing við at seta eitt siffur
framman fyri 9-talið í hvørjari uppgávu.
Í staðin fyri 9+2 kunnu næmingarnir t.d.
rokna 29+2. Á aðru reglu skulu tey so
skriva 29+1+1. Á triðju reglu skulu tey
so skriva 30+1=31.
Annað virksemi
Spæl:Talveiða
Lag et flere ganger.
Ger eina talvu við 10 x 10 puntum á eitt
A4-ark ella brúka Avritssíðu 3.20 í
Avrits­mappu 1–4. Skriva tølini frá 1 til 9 í
puntarnar í tilvildarligari raðfylgju og
avrita eitt eintak til hvønn næming.
Næmingarnir skulu hava litblýantar í
ymiskum litum. Tey kunnu t.d. byrja við
einum reyðum blýanti. Lærarin sigur eitt
tal millum 10 og 20, t.d. 14. So skulu
næmingarnir finna tøl, sum standa lið
um lið tvørturum ella upp og niður, og
sum til samans verða 14. Tað ber væl til
at brúka fleiri enn 2 tøl, men øll tølini
skulu hanga saman (ikki á skák).
Næm­ingarnir seta ring um tey tølini,
sum teir finna. Tað ber ikki til at brúka
sama tal fleiri ferðir, so leingi sum
næm­ing­ar­nir finna summin 14 við tí
reyða blýantinum.
Næmingarnir fáa um leið ein minutt
at leita í, so sigur lærarin steðga (kann
eisini vera longur). Nú skulu næm­ing­ar­
nir taka ein blýant við einum øðrum liti,
t.d. bláan. Lærarin sigur eitt annað tal,
t.d. 17, og næmingarnir fáa ein minutt at
leita eftir tølum, sum til samans verða
17. Nú kunnu tey eisini brúka tøl, sum
vórðu brúkt við tí reyða blýantinum í
fyrra umfari.
At enda kunnu næmingarnir telja, hvussu
ofta tey fingu talið, sum tey skuldu leita
eftir.
ein eggjabakka (ella tílíkt), har pláss er
fyri tíggju eggum (brikkum). 9+4 verður
tá loyst við at leggja 9 „egg“ í bakkan og
taka 4 afturat. Eitt av teimum fýra
passar í bakkan, hini trý eru leys. Til
samans verða tað 10+3=13 egg. Vís
næm­ingunum, hvussu tað, sum tey hava
gjørt við ítøkiligum lutum, hevur
sam­band við tær skriv­ligu uppgávurnar í
bók­ini. Tað ber eisini til at nýta
tekningar av tíggjara­bólkum og seta
kross á, sí Avrits­síðu 45 í Avritsmappu
1–4 .
Ein annar máti er at nýta perluband at
loysa uppgávurnar. 9+4 verður tá loyst
við fyrst at finna níggju kúlur og so telja
fýra afturat og seta eina klemmu har. At
enda hyggja næmingarnir, hvussu nógvar
kúlur so eru vinstru­megin klemmuna.
Eisini eigur lærarin at vísa teimum,
hvussu hetta hevur samband við tær
skrivligu uppgávurnar: Vit roknaðu 9+4, og
so at vit fáa ein tíggjara við at taka 1 frá
hinum talinum. Harvið verður 3 tikið
sundur í 1+2, 6 í 1+5, 2 í 1 +1 o.s.fr.
Ger ein tíggjara og rokna
Næmingarnir venja seg at brúka
framferðarháttin til høvuðrokning, sum er
vístur omanfyri. Lat tey vísa, hvussu tey
hugsa, bæði við at „flyta“ brikkar og við at
skriva tøl á tær tómu strikurnar.
Ger ein tíggjara og rokna
Eins og uppgáva 2, men hesaferð
hava næmingarnir onga tekning av
eggjabakkanum við brikkum at styðja
seg til. Tey, sum duga, loysa hesa
upp­gávu­na við tølunum einsamøllum.
Einfaldari
Lat næmingarnar nýta ítøkiligar lutir at
loysa uppgávurnar. Ein máti er at brúka
Eftirsum vit brúktu 1 fyri at fáa fullan
tíggjara, eru 3 eftir, tí at 1+3=4.
GG! Hetta snýr seg um at læra ein
framferðarhátt í høvuðrokning. Tað
merkir í fyrra lagi, at næmingarnir ikki
bara skulu finna svarið á uppgávunum.
Kanska duga tey líka skjótt at telja seg
fram til rætta svarið, men her ræður um,
at tey gera – og skriva – eina millum­
rokning. Í øðrum lagi er tað ikki
mein­ing­in, at næmingarnir skulu læra
hetta sum ein skrivligan máta at rokna
additións­upp­gávur seinni. Hetta er ein
fram­ferðar­háttur, sum setur stór krøv til
næm­ing­arnar við tað, at hann er í fleiri
stigum. Tí hava vit her (og eisini seinni í
2a) eina eyka reglu at styðja okkum til, so
at næm­ing­arnir kunnu loysa uppgávuna
stig fyri stig. Fyrsta stig er at finna
tíggjaravinin hjá tí fyrra talinum, og so
taka tað seinna talið sundur eftir tí. Í
øllum uppgávunum er tað fyrra talið 9,
peikar á ein mynt fyri og annan eftir:
tíggju, tjúgu, tríati, fjøruti, fimmti, seksti,
sjeyti, áttati, níti, hundrað.
 Síða 39
Samrøðumynd um
additión við tíggjaraskifti
Her verður víst á ein framferðarhátt í
høvuðrokning, har tvey eittsifrað tøl
verða løgd saman við fyrst at leggja
aftur at tí fyrra talinum, so tað verður
ein tíggjari. Tað verður víst við teimum
báðum eggjabakkunum ovast á síðuni.
Vit rokna 9+4 við fyrst at rokna 9+1.
Fyri at kunna gera tað, mugu
næmingarnir duga tíggjaravinirnar. Tey
mugu vita, at tá ið tað fyrra talið er 9, so
restar eitt í at koma upp í 10. Síðan
leggja næmingarnir tey 3, sum eftir eru,
afturat og finna svarið við at rokna
10+3=13. Fyri at kunna gera tað, mugu
næmingarnir duga talvinirnar hjá fýra:
Hvat er at gera?
 Síða 38
Ger tíggjara og skriva
tølini
Set ring um tíggju av eggunum og skriva
talið sum ein tíggjari pluss eittarar.
Næmingarnir skulu eisini skriva
sundurtøkuna av 14 í talsirklarnar.
Tá ið tikið verður saman um hesa
síðuna, hevur tað týdning at tosa við
næm­ingarnar um, hví tað er hent at býta
sundur í tíggjarar. Tá verður lættari at
telja, hvussu nógv eru til samans. Hetta
sæst enn betur, tá ið talan er um størri
tøl.
Vit mugu eisini leggja dent á, at tá ið
vit skriva eitt tal, t.d. 13, umboðar sifrið
1 ein tíggjara, altso 10, og ikki ein
eitt­ara. Royn at fáa næmingarnar at
hugsa um hetta. Legg t.d.16 brikkar á
uppvørpu ella samvirkna talvu ella tekna
16 sirklar á talvuna:
n Nú havi eg lagt/teknað nakrar brikkar
her. Dugir onkur at telja, hvussu nógvir
teir eru? (Bið ein næming koma fram at
telja, altso 16.)
n Kanst tú skriva talið á talvuna?
(Næmingurin skrivar 16.) Tú hevur fyrst
skrivað eitt eitttal og so eitt sekstal. Men
hvørjum er tað eitt av, og hvørjum er tað
seks av? Hvat hevur tað at gera við talið
á brikkum?
Ger ein tíggjara
og skriva tølini
Á sama hátt sum í uppgávu 1 skulu
næmingarnir seta ring um 10 egg. Talið
til samans skal verða skrivað sum
tíggjarar og eittarar.
Í tí seinastu uppgávuni verða tveir
tíggjarar og eingir eittarar. Vís á, at tað er
tí, at eitt null stendur aftast í 20.
Í arbeið­inum við hesari og teimum
komandi síðunum eiga næmingarnir at
læra seg at telja tíggjarar upp í hundrað.
Tað kunnu tit gera við at tekna tíggju
tíggjukrónur á talvuna og so telja hart í
felag, hvussu nógvum krónum mynd er
av, meðan lærarin ella ein næm­ingur
38 2 • Pluss og minus við tølunum upp í 20
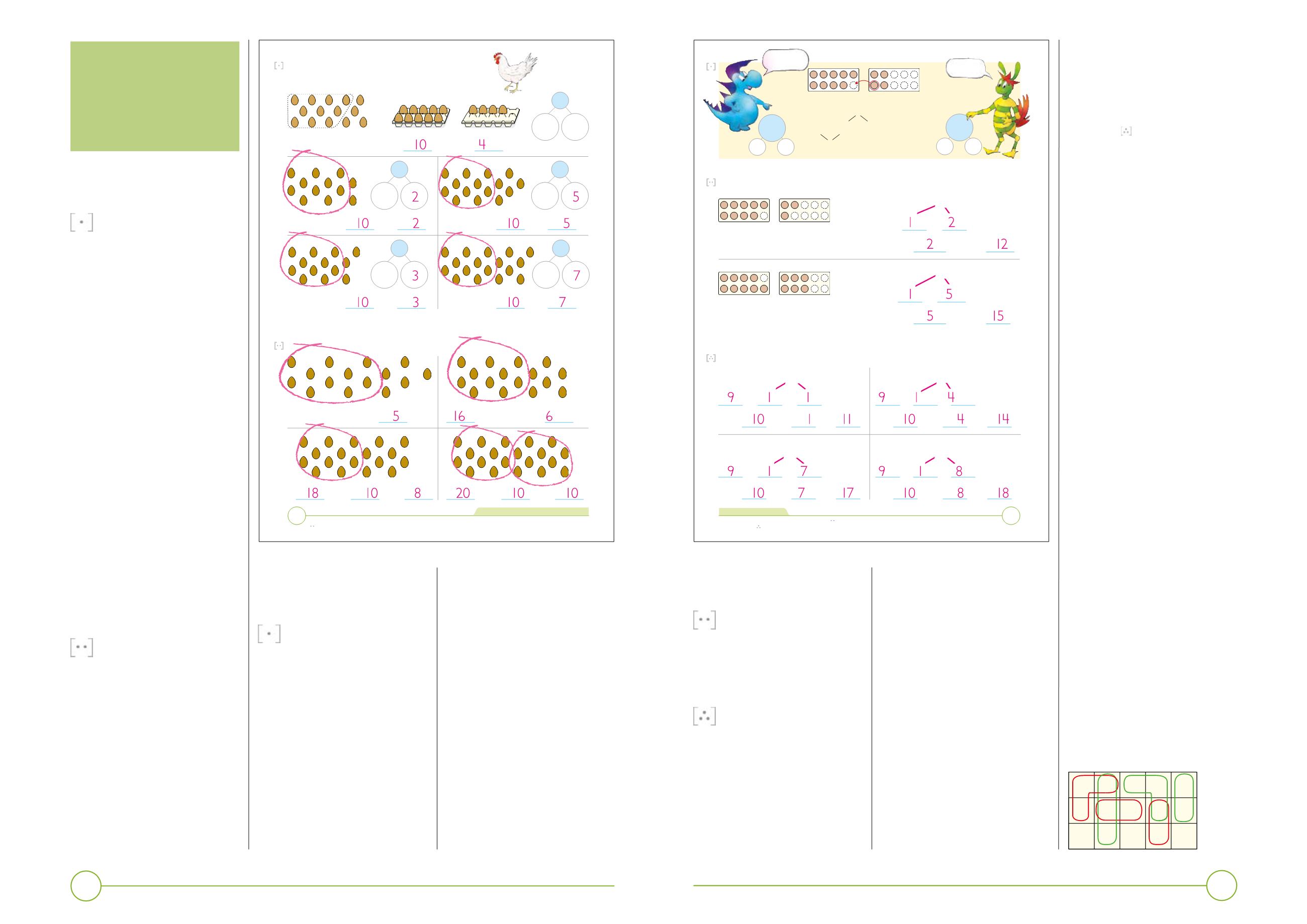
• Set ring um 10 egg og skriva talið sum ein tíggjara og restina sum eittarar. Skriva eisini tøl í sirklarnar.
Set ring um 10 egg og skriva talið sum ein tíggjara og restina sum eittarar.
Ger ein tíggjara og finn restina.
Ger ein tíggjara og skriva tølini.
14 = +
12 = + 15 = +
13 = + 17 = +
15 = 10 + = 10 +
= + = +
4 10
14
10
15
10
12
10
13
10
17
www.snar.fo/rokning 39
• Samrøðumynd um samanlegging við tíggjaraskifti. Tak sundur annað talið í roknistykkinum, soleiðis at tú fært ein tíggjara,
og legg saman. Tak sundur annað talið í roknistykkinum, soleiðis at tú fært ein tíggjara, og legg saman.
Ger ein tíggjara og rokna.
Ger ein tíggjara og rokna.
9 + 4 =
9 + 1 + 3 =
10 + 3 = 13
9 + 3 =
9 + + =
10 + =
9 + 6 =
9 + + =
10 + =
9 + 2 =
+ + =
+ =
9 + 5 =
+ + =
+ =
9 + 8 =
+ + =
+ =
9 + 9 =
+ + =
+ =
3 1
4
Eg taki 4
sundur í 1 og 3.
1 9
10
Eg geri
ein tíggjara.
3 7 7 4 9
3 8 5 6 8
6 2 2 7 5
Støddfrøðiligt innihald
n Bólka í tíggjarar
n Taka sundur í tíggjarar og
eittarar
n Høvuðrokning: leggja eittsifrað
tøl saman, við tíggjaraskifti